Elíptica_Criptografía
Python
Publicado el 27 de Noviembre del 2024 por Hilario (144 códigos)
548 visualizaciones desde el 27 de Noviembre del 2024
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
---------------------------------------------------------------------------------------------------------------------------
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
Aula_28_Nov_Eliptica_Criptografia.py
+++++++++++++++++++++++++++++
Dentro de todas las partes, digamos, técnologicas, que hemos ido estudiando y procesando. Comenzamos un tema nuevo,
para el que seguiremos utilizando el lengua Python, y un sistema operativo basado en linux.
Nos adentramos en el mundo de la criptografía y de las claves, en principio, en los sistemas más utilizados
por el secure shel SSH, en principio con un ejemplo sencillo, que intentaré explicar lo mejor posible.
Como siempre, en nuestras sucesivas clases de técnología iremos aclarando las dudas que surjan, lo que supondrá, como siempre
ocurre en nuestras clases, profundizar mucho más sobre el tema. Os pido, que dentro de lo posible, intenteis razonar el código.
Luego ya aclararemos todo lo que surja, pero es más fácil su comprensión si llevamos, digamos, trillado, un poco de lo que se trata.
EMPECEMOS:
++++++++++++++
-¿Qué es una curva elíptica?
Una curva elíptica es una curva matemática que tiene la forma general:
y2=x3+ax+b (Ya sabeis, y elevado a 2, igual a x elevado a 3, más a por x, más b)
Esta curva tiene propiedades interesantes que se aprovechan en criptografía para generar claves. En criptografía de curvas elípticas (ECC, por sus siglas en inglés), usamos puntos sobre esta curva para construir un sistema de claves.
¿Cómo se construyen las claves con una curva elíptica?
1. Selección de la curva elíptica:
◦ Primero, se elige una curva elíptica específica. La ecuación y2=x3+ax+b tiene parámetros como a, b, y un número primo p que define el campo finito (es decir, trabajamos con números que están "limitados" por un número p).
◦ Un ejemplo común de curva elíptica es la curva secp256k1, que se usa en Bitcoin.
2. Punto generador (G):
◦ Sobre la curva elíptica, hay un punto generador G que es un punto específico de la curva, que se conoce de antemano. Este punto sirve para generar las claves.
3. Clave privada:
◦ La clave privada es un número aleatorio que se elige de manera segura. Es como una "semilla" que vamos a usar para generar la clave pública.
◦ Este número privado es secreto, y nunca se debe compartir.
4. Clave pública:
◦ La clave pública se genera multiplicando el punto generador G por el número privado (clave privada). Esto se hace mediante una operación llamada multiplicación escalar.
◦ Matemáticamente, si tienes una clave privada k, la clave pública P es: P=k⋅G
◦ Aquí, P es un nuevo punto sobre la curva que depende de k y G. Es casi imposible calcular k solo a partir de P, lo que hace la curva elíptica segura para su uso en criptografía.
5. Uso en criptografía:
◦ En criptografía de clave pública, puedes usar la clave pública para verificar la autenticidad de un mensaje o para cifrar datos.
◦ Solo la persona que tiene la clave privada puede descifrar los datos o firmar mensajes, porque se necesita la clave privada para generar la firma o descifrar.
Ejemplo práctico en criptografía
Imagina que quieres enviar un mensaje seguro a alguien:
1. La otra persona te envía su clave pública.
2. Tú usas esa clave pública para cifrar el mensaje.
3. La otra persona usa su clave privada para descifrarlo.
Y cuando firmes un mensaje:
1. Usas tu clave privada para firmar el mensaje (de forma que solo tú puedas hacerlo).
2. Cualquier persona que tenga tu clave pública puede verificar que la firma es auténtica y que no ha sido modificada.
¿Por qué es segura?
La seguridad de este sistema se basa en que, aunque la multiplicación escalar de un número por un punto en la curva es fácil de hacer, el proceso inverso (saber la clave privada a partir de la clave pública) es extremadamente difícil. Este problema se llama el problema del logaritmo discreto, y es la base de la seguridad de las curvas elípticas.
En fin, alumnos, resumiendo:
1. Clave privada: Número secreto que eliges.
2. Clave pública: Punto en la curva generado a partir de la clave privada.
3. Suma de puntos: Usada para multiplicar el punto generador G para obtener la clave pública.
4. Seguridad: Es muy difícil calcular la clave privada a partir de la clave pública.
Este enfoque se usa en criptografía moderna para asegurar comunicaciones y transacciones, como en Bitcoin o en protocolos TLS/SSL para la navegación segura por Internet.
----------------------------------------------------------------------------------------------------------------------------------
Bien, después de esta pequeña introducción, que ampliaremos en clase, la próxima semana y sucesivas, vamos con algo más práctico:
1. Representación gráfica de la curva elíptica.
---------------------------------------------------------------
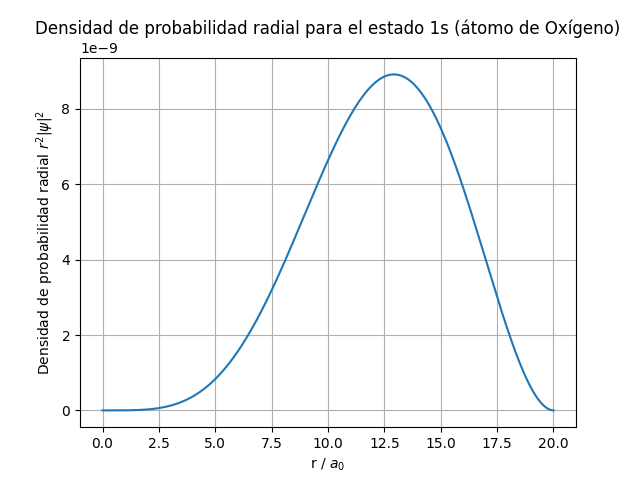
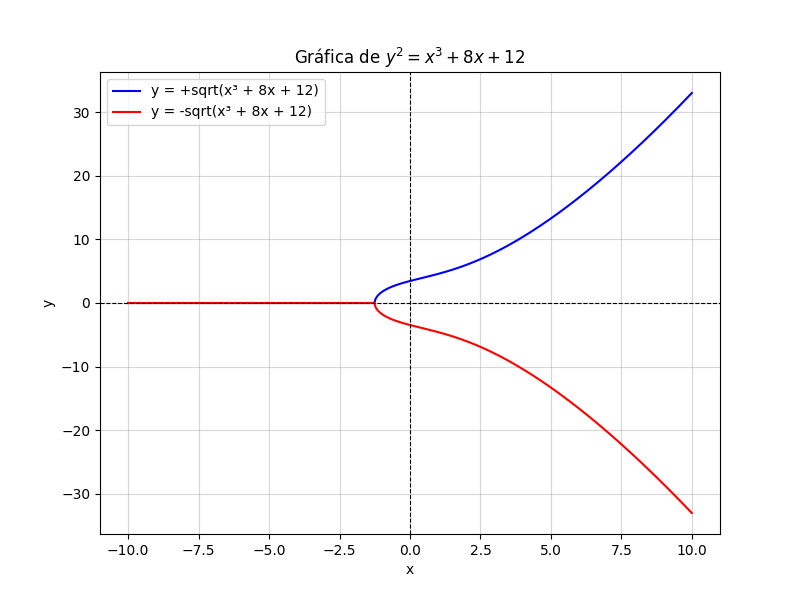
El programa comienza generando una gráfica de la curva elíptica definida por y2=x3+8x+12 sobre los números reales:
• Cálculo de y2:
La ecuación se evalúa para valores de x en un rango definido [−10,10] para obtener los valores de y2.
• Raíces cuadradas positivas y negativas:
La raíz cuadrada de y2 se toma tanto positiva como negativa (y=±y2) para trazar ambas ramas de la curva.
• Visualización:
Usa matplotlib para graficar las ramas positiva y negativa en colores distintos. También incluye líneas de referencia para los ejes x e y, junto con una cuadrícula para mejorar la legibilidad.
Propósito:
Este gráfico permite entender visualmente la forma de una curva elíptica sobre los números reales antes de trabajar con el caso modular (campo finito).
2. Implementación de una curva elíptica modular (campo finito pequeño)
-------------------------------------------------------------------------------------------------------
En esta sección, se define una clase EllipticCurve para manejar operaciones básicas en una curva elíptica sobre un campo finito
Fp:
• Parámetros de la curva:
La curva está definida por y2=x3+ax+bmodp, donde:
◦ a=8, b=12, y p=97 (un número primo que define el campo).
• Validación de singularidades:
Verifica que la curva no sea singular usando la condición 4a3+27b2=0modp.
• Operaciones básicas:
◦ Pertenencia a la curva: Verifica si un punto (x,y) está en la curva.
◦ Suma de puntos: Implementa la adición de puntos, considerando casos como:
▪ P+O=P (punto identidad).
▪ Suma de puntos distintos.
▪ Duplicación de un punto (derivada de la tangente).
◦ Multiplicación escalar: Repite la suma k⋅P usando el algoritmo de duplicación y adición.
• Generación de claves:
◦ Se generan todos los puntos válidos en la curva para el campo F97.
◦ Selecciona un punto generador G (el primero de la lista).
◦ La clave privada es un entero aleatorio entre 1 y p−1.
◦ La clave pública es el resultado de k⋅G, donde k es la clave privada.
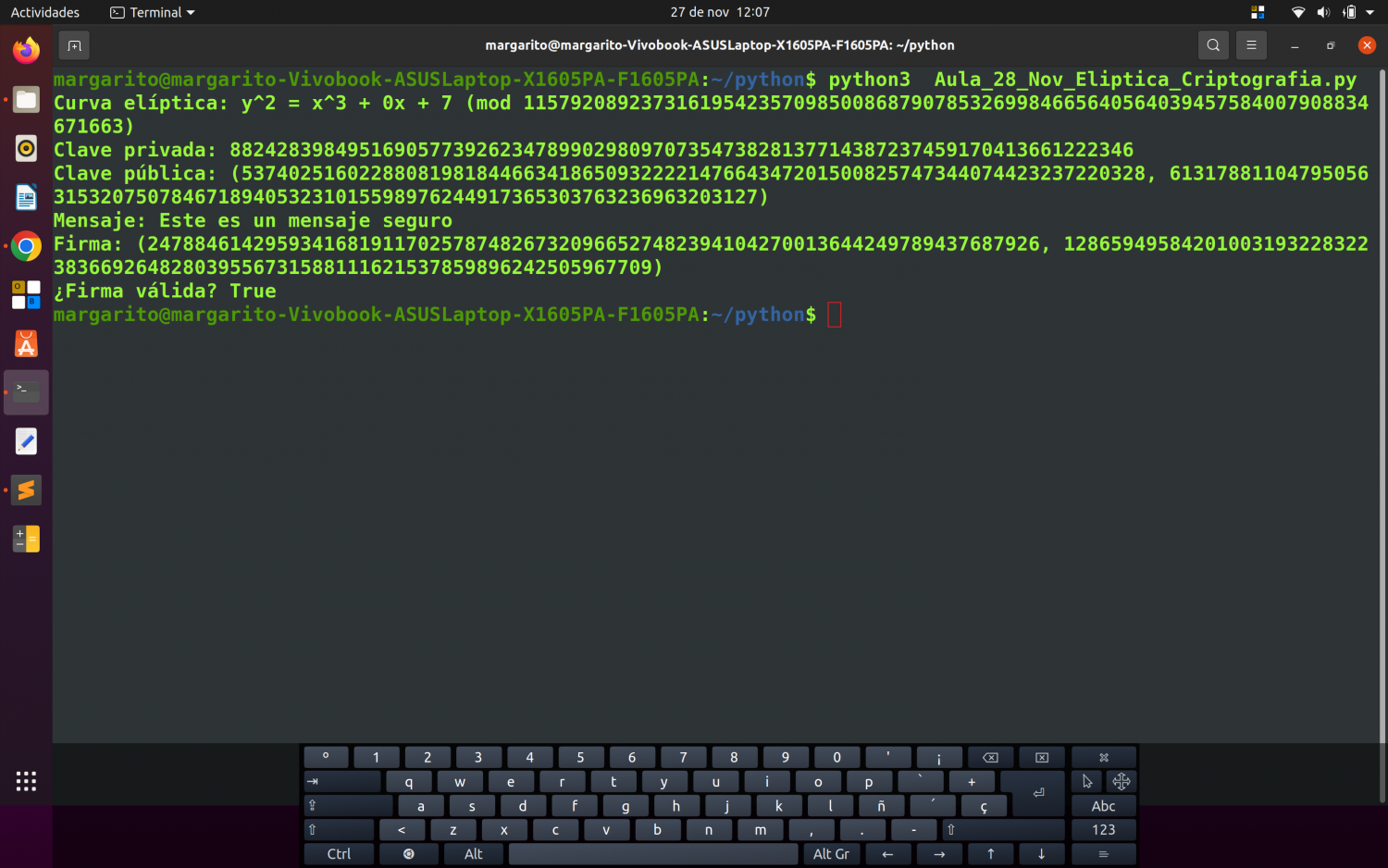
Resultados:
Imprime:
• La ecuación de la curva modular.
• El punto generador G.
• Las claves privada y pública generadas.
3. Criptografía realista con secp256k1
Esta sección introduce una curva elíptica de uso práctico en criptografía, secp256k1, utilizada por Bitcoin:
• Definición:
La curva está definida por y2=x3+7modp, donde:
◦ p es un número primo grande (2256−232−977).
◦ G es un punto generador predeterminado en la curva.
◦ n es el orden del punto generador.
• Operaciones similares:
Implementa las mismas operaciones (pertenencia, suma de puntos, multiplicación escalar) adaptadas a los parámetros de secp256k1.
• Generación de claves:
◦ La clave privada es un número aleatorio de hasta 256 bits (1≤k<n).
◦ La clave pública es k⋅G, donde G y n aseguran un espacio de claves inmenso y seguridad criptográfica.
Resultados:
Muestra:
• La ecuación de secp256k1.
• El punto generador G.
• Las claves privada y pública.
Como véis, queridos alumnos, el propósito formativo del programa es:
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
1. Introducción visual a las curvas elípticas:
La gráfica inicial ayuda a entender cómo luce una curva elíptica y su simetría sobre los números reales.
2. Conceptos básicos de curvas elípticas en campos finitos:
◦ Explica cómo las curvas se definen y operan en un espacio modular, con un ejemplo simple (p=97).
◦ Introduce operaciones críticas como suma de puntos y multiplicación escalar.
3. Aplicación práctica en criptografía:
◦ Usa una curva criptográfica estándar (secp256k1) para mostrar cómo generar claves privadas y públicas.
◦ Destaca las diferencias entre un ejemplo educativo y un caso práctico con parámetros reales.
Bien, y como posibles mejoras, vamos a implementar lo siguiente:
---------------------------------------------------------------
• Implementar firmas digitales (ECDSA) como extensión práctica.
• Mostrar cómo la clave pública se convierte en un formato útil (como direcciones en Bitcoin).
• Incluir explicaciones más detalladas sobre seguridad y resistencia frente a ataques.
Comoos lo expuesto, tengo por sentado que os resultará un tanto farragoso, deseo que, como ya dije, comencéis su estudio-
Iremos puliendo dudas, y asentando conceptos los próximos días.
///////////////////////////////////////////////////////////////////////////
Como casi todos los ejercicios, este fue realizado, bajo una plataforma Linux,
en concreto con Ubuntu 20.04.6 LTS.
Fue editado con Sublime Text.
Se utilizó, Python3.
Y como smpre indico, se deberán de tener cargadas en el sistema, todas las librerias
que el código pide importar para su ejecucucíon.
Comando de ejecucuón bajo consola linux:
python3 Aula_28_Nov_Eliptica_Criptografia.py

---------------------------------------------------------------------------------------------------------------------------

////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
Aula_28_Nov_Eliptica_Criptografia.py
+++++++++++++++++++++++++++++
Dentro de todas las partes, digamos, técnologicas, que hemos ido estudiando y procesando. Comenzamos un tema nuevo,
para el que seguiremos utilizando el lengua Python, y un sistema operativo basado en linux.
Nos adentramos en el mundo de la criptografía y de las claves, en principio, en los sistemas más utilizados
por el secure shel SSH, en principio con un ejemplo sencillo, que intentaré explicar lo mejor posible.
Como siempre, en nuestras sucesivas clases de técnología iremos aclarando las dudas que surjan, lo que supondrá, como siempre
ocurre en nuestras clases, profundizar mucho más sobre el tema. Os pido, que dentro de lo posible, intenteis razonar el código.
Luego ya aclararemos todo lo que surja, pero es más fácil su comprensión si llevamos, digamos, trillado, un poco de lo que se trata.
EMPECEMOS:
++++++++++++++
-¿Qué es una curva elíptica?
Una curva elíptica es una curva matemática que tiene la forma general:
y2=x3+ax+b (Ya sabeis, y elevado a 2, igual a x elevado a 3, más a por x, más b)
Esta curva tiene propiedades interesantes que se aprovechan en criptografía para generar claves. En criptografía de curvas elípticas (ECC, por sus siglas en inglés), usamos puntos sobre esta curva para construir un sistema de claves.
¿Cómo se construyen las claves con una curva elíptica?
1. Selección de la curva elíptica:
◦ Primero, se elige una curva elíptica específica. La ecuación y2=x3+ax+b tiene parámetros como a, b, y un número primo p que define el campo finito (es decir, trabajamos con números que están "limitados" por un número p).
◦ Un ejemplo común de curva elíptica es la curva secp256k1, que se usa en Bitcoin.
2. Punto generador (G):
◦ Sobre la curva elíptica, hay un punto generador G que es un punto específico de la curva, que se conoce de antemano. Este punto sirve para generar las claves.
3. Clave privada:
◦ La clave privada es un número aleatorio que se elige de manera segura. Es como una "semilla" que vamos a usar para generar la clave pública.
◦ Este número privado es secreto, y nunca se debe compartir.
4. Clave pública:
◦ La clave pública se genera multiplicando el punto generador G por el número privado (clave privada). Esto se hace mediante una operación llamada multiplicación escalar.
◦ Matemáticamente, si tienes una clave privada k, la clave pública P es: P=k⋅G
◦ Aquí, P es un nuevo punto sobre la curva que depende de k y G. Es casi imposible calcular k solo a partir de P, lo que hace la curva elíptica segura para su uso en criptografía.
5. Uso en criptografía:
◦ En criptografía de clave pública, puedes usar la clave pública para verificar la autenticidad de un mensaje o para cifrar datos.
◦ Solo la persona que tiene la clave privada puede descifrar los datos o firmar mensajes, porque se necesita la clave privada para generar la firma o descifrar.
Ejemplo práctico en criptografía
Imagina que quieres enviar un mensaje seguro a alguien:
1. La otra persona te envía su clave pública.
2. Tú usas esa clave pública para cifrar el mensaje.
3. La otra persona usa su clave privada para descifrarlo.
Y cuando firmes un mensaje:
1. Usas tu clave privada para firmar el mensaje (de forma que solo tú puedas hacerlo).
2. Cualquier persona que tenga tu clave pública puede verificar que la firma es auténtica y que no ha sido modificada.
¿Por qué es segura?
La seguridad de este sistema se basa en que, aunque la multiplicación escalar de un número por un punto en la curva es fácil de hacer, el proceso inverso (saber la clave privada a partir de la clave pública) es extremadamente difícil. Este problema se llama el problema del logaritmo discreto, y es la base de la seguridad de las curvas elípticas.
En fin, alumnos, resumiendo:
1. Clave privada: Número secreto que eliges.
2. Clave pública: Punto en la curva generado a partir de la clave privada.
3. Suma de puntos: Usada para multiplicar el punto generador G para obtener la clave pública.
4. Seguridad: Es muy difícil calcular la clave privada a partir de la clave pública.
Este enfoque se usa en criptografía moderna para asegurar comunicaciones y transacciones, como en Bitcoin o en protocolos TLS/SSL para la navegación segura por Internet.
----------------------------------------------------------------------------------------------------------------------------------
Bien, después de esta pequeña introducción, que ampliaremos en clase, la próxima semana y sucesivas, vamos con algo más práctico:
1. Representación gráfica de la curva elíptica.
---------------------------------------------------------------
El programa comienza generando una gráfica de la curva elíptica definida por y2=x3+8x+12 sobre los números reales:
• Cálculo de y2:
La ecuación se evalúa para valores de x en un rango definido [−10,10] para obtener los valores de y2.
• Raíces cuadradas positivas y negativas:
La raíz cuadrada de y2 se toma tanto positiva como negativa (y=±y2) para trazar ambas ramas de la curva.
• Visualización:
Usa matplotlib para graficar las ramas positiva y negativa en colores distintos. También incluye líneas de referencia para los ejes x e y, junto con una cuadrícula para mejorar la legibilidad.
Propósito:
Este gráfico permite entender visualmente la forma de una curva elíptica sobre los números reales antes de trabajar con el caso modular (campo finito).
2. Implementación de una curva elíptica modular (campo finito pequeño)
-------------------------------------------------------------------------------------------------------
En esta sección, se define una clase EllipticCurve para manejar operaciones básicas en una curva elíptica sobre un campo finito
Fp:
• Parámetros de la curva:
La curva está definida por y2=x3+ax+bmodp, donde:
◦ a=8, b=12, y p=97 (un número primo que define el campo).
• Validación de singularidades:
Verifica que la curva no sea singular usando la condición 4a3+27b2=0modp.
• Operaciones básicas:
◦ Pertenencia a la curva: Verifica si un punto (x,y) está en la curva.
◦ Suma de puntos: Implementa la adición de puntos, considerando casos como:
▪ P+O=P (punto identidad).
▪ Suma de puntos distintos.
▪ Duplicación de un punto (derivada de la tangente).
◦ Multiplicación escalar: Repite la suma k⋅P usando el algoritmo de duplicación y adición.
• Generación de claves:
◦ Se generan todos los puntos válidos en la curva para el campo F97.
◦ Selecciona un punto generador G (el primero de la lista).
◦ La clave privada es un entero aleatorio entre 1 y p−1.
◦ La clave pública es el resultado de k⋅G, donde k es la clave privada.
Resultados:
Imprime:
• La ecuación de la curva modular.
• El punto generador G.
• Las claves privada y pública generadas.
3. Criptografía realista con secp256k1
Esta sección introduce una curva elíptica de uso práctico en criptografía, secp256k1, utilizada por Bitcoin:
• Definición:
La curva está definida por y2=x3+7modp, donde:
◦ p es un número primo grande (2256−232−977).
◦ G es un punto generador predeterminado en la curva.
◦ n es el orden del punto generador.
• Operaciones similares:
Implementa las mismas operaciones (pertenencia, suma de puntos, multiplicación escalar) adaptadas a los parámetros de secp256k1.
• Generación de claves:
◦ La clave privada es un número aleatorio de hasta 256 bits (1≤k<n).
◦ La clave pública es k⋅G, donde G y n aseguran un espacio de claves inmenso y seguridad criptográfica.
Resultados:
Muestra:
• La ecuación de secp256k1.
• El punto generador G.
• Las claves privada y pública.
Como véis, queridos alumnos, el propósito formativo del programa es:
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
1. Introducción visual a las curvas elípticas:
La gráfica inicial ayuda a entender cómo luce una curva elíptica y su simetría sobre los números reales.
2. Conceptos básicos de curvas elípticas en campos finitos:
◦ Explica cómo las curvas se definen y operan en un espacio modular, con un ejemplo simple (p=97).
◦ Introduce operaciones críticas como suma de puntos y multiplicación escalar.
3. Aplicación práctica en criptografía:
◦ Usa una curva criptográfica estándar (secp256k1) para mostrar cómo generar claves privadas y públicas.
◦ Destaca las diferencias entre un ejemplo educativo y un caso práctico con parámetros reales.
Bien, y como posibles mejoras, vamos a implementar lo siguiente:
---------------------------------------------------------------
• Implementar firmas digitales (ECDSA) como extensión práctica.
• Mostrar cómo la clave pública se convierte en un formato útil (como direcciones en Bitcoin).
• Incluir explicaciones más detalladas sobre seguridad y resistencia frente a ataques.
Comoos lo expuesto, tengo por sentado que os resultará un tanto farragoso, deseo que, como ya dije, comencéis su estudio-
Iremos puliendo dudas, y asentando conceptos los próximos días.
///////////////////////////////////////////////////////////////////////////
Como casi todos los ejercicios, este fue realizado, bajo una plataforma Linux,
en concreto con Ubuntu 20.04.6 LTS.
Fue editado con Sublime Text.
Se utilizó, Python3.
Y como smpre indico, se deberán de tener cargadas en el sistema, todas las librerias
que el código pide importar para su ejecucucíon.
Comando de ejecucuón bajo consola linux:
python3 Aula_28_Nov_Eliptica_Criptografia.py