Código de Python - Partículas

****************************************************************************************************************
Aula_18_Apli_Sep_Schrodinger_Oxigeno.py
***************************************

Proponemos, para el Aula 18, dentro del tema de la ecuación de Schrödinger, una aplicación realizada en lenguaje Python, donde aplicamos la ecuación de Schrödinger, para determinar la posible posicion sobre un electrón de la primera capa en un átomo de Oxigeno.

Explicación del Código

Parámetros y constantes:
Se definen las constantes físicas necesarias como la constante de Planck reducida (hbar), la carga del electrón (e), la masa del electrón (m_e), la permitividad del vacío (epsilon_0), y el número atómico del oxígeno (Z = 8).

Malla radial: Se crea una malla en el espacio radial para resolver la ecuación diferencial utilizando el método de diferencias finitas.

Potencial coulombiano: Se calcula el potencial de Coulomb debido al núcleo, que es la parte central de la energía potencial en el sistema.

Matriz Hamiltoniana: Se construye la matriz Hamiltoniana usando diferencias finitas.
Resolución de la ecuación de Schrödinger: Se obtienen los autovalores y autovectores de la matriz Hamiltoniana. El autovalor más bajo corresponde a la energía del estado fundamental (1s).

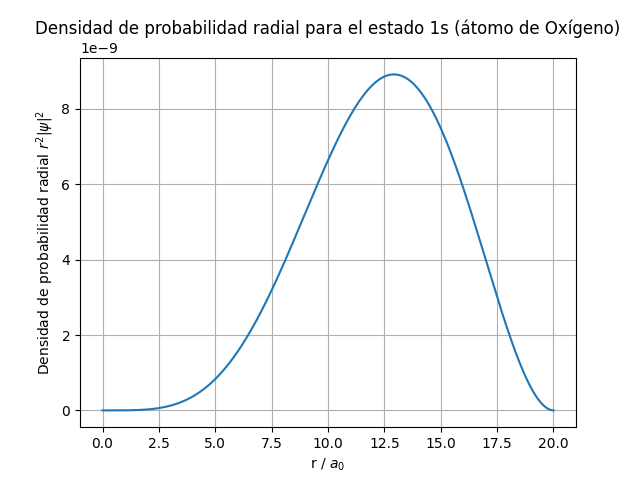
Normalización y cálculo de la probabilidad radial: La función de onda se normaliza y se calcula la densidad de probabilidad radial.

Gráfica: Se grafica la densidad de probabilidad radial en función de la distancia radial.
Consideraciones
Este código resuelve la ecuación de Schrödinger para un electrón en un campo de Coulomb, que es una aproximación simplificada para el átomo de hidrógeno. Para el átomo de oxígeno, este modelo no considera las interacciones electrón-electrón ni la repulsión entre electrones, pero proporciona una idea básica sobre la distribución de probabilidad de un electrón en el orbital 1s.

Este programa aplica muy básicamente la ecuación Schrödinger, explicando una forma de iniciación
que resuelve la posivilidad probabilistica de encontrar la párticula, como se puede ver en el gráfico resultante.

Durante el código, explicamos lo más conciso posible los pasos más importantes. En el aula, durante la segunda semana de spetiembre trataremos de explicar el resto de las dudas, así como aumentar la complejidad del
código para acercarlo lo más posible a la realidad CUÁNTICA.

-----------------------------------------------------------------------------------------------------
Programa realizado bajo Linux, sistema operativo: Ubuntu 20.04.6 LTS.
Editor Sublime text.
Ejecución:python3 Aula_18_Apli_Sep_Schrödinger_Oxigeno.py