Iniciar sesiónCerrar
Correo:
Contraseña:
Entrar
Recordar sesión en este navegador
Iniciar sesiónIniciar sesiónCrear cuentaCrear cuenta
LWP » Código Fuente » es

Mostrar los tags: es

Volver
Agregar Código Fuente
Mostrando del 11 al 20 de 734 coincidencias
<<>>
Se ha buscado por el tag: es
Imágen de perfil

Red-CNN Detección de bordes


Python

Publicado el 19 de Febrero del 2024 por Hilario (144 códigos)
431 visualizaciones desde el 19 de Febrero del 2024
Figure_1
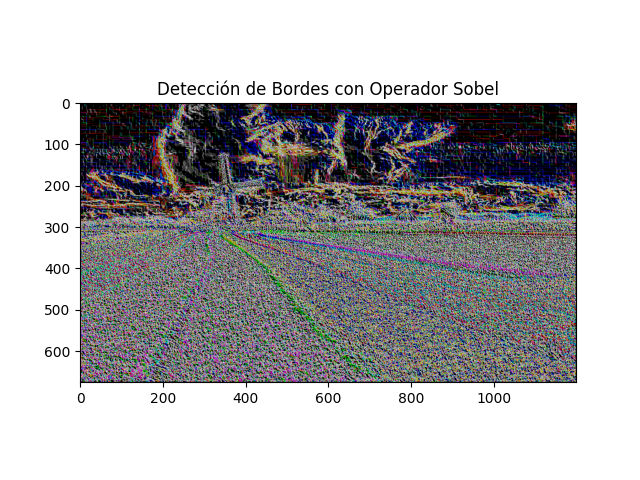
Figure_2

Los kernels Sobel son filtros utilizados comúnmente en procesamiento de imágenes para realizar operaciones de convolución, especialmente en el contexto de detección de bordes. Estos filtros están diseñados para resaltar cambios rápidos en la intensidad de los píxeles en una imagen, lo que generalmente indica la presencia de bordes.

El operador Sobel consiste en dos kernels, uno para la detección de cambios horizontales y otro para cambios verticales. Estos kernels son matrices pequeñas que se aplican a la imagen mediante la operación de convolución. Los kernels Sobel comúnmente utilizados son los siguientes:

Kernel Sobel para detección de bordes horizontales (kernel_sobel_x):

[ -1, 0, 1]
[ -2, 0, 2]
[ -1, 0, 1]

Kernel Sobel para detección de bordes verticales (kernel_sobel_y):

[ 1, 2, 1]
[ 0, 0, 0]
[-1, -2, -1]

La operación de convolución implica deslizar estos kernels sobre la imagen original, multiplicando los valores de los píxeles en la región correspondiente del kernel y sumándolos para obtener un nuevo valor en la posición central. Este proceso se repite para cada píxel en la imagen, generando así dos nuevas imágenes filtradas: una resaltando cambios horizontales y otra resaltando cambios verticales.

La magnitud de los bordes se calcula combinando las respuestas horizontales y verticales mediante una fórmula de magnitud Euclidiana.

Este resultado proporciona una representación de la intensidad de los bordes en la imagen original, lo cual es útil para tareas como detección de contornos. En el código que compartiste anteriormente, estos kernels Sobel se utilizan para realizar la detección de bordes en la imagen cargada.


Este programa en Python: python3 Aula_28_bordes_CNN.py, realiza la detección de bordes en una imagen utilizando el operador Sobel. Aquí tienes una explicación paso a paso:

Cargar la imagen:
Utiliza la biblioteca OpenCV (cv2) para cargar una imagen desde la ruta "/home/margarito/python/tulipanes.jpeg".
Verifica si la carga de la imagen fue exitosa.

Convertir la imagen a formato RGB:
Utiliza la función cv2.cvtColor para convertir la imagen cargada (en formato BGR) a formato RGB.
Muestra la imagen original utilizando la biblioteca matplotlib.

Definir los kernels Sobel:
Define dos kernels Sobel, uno para la detección de bordes horizontales (kernel_sobel_x) y otro para la detección de bordes verticales (kernel_sobel_y).

Aplicar los filtros Sobel:
Utiliza la función cv2.filter2D para aplicar los filtros Sobel a la imagen original, obteniendo dos imágenes resultantes (imagen_bordes_x e imagen_bordes_y), que representan los bordes horizontales y verticales, respectivamente.

Calcular la magnitud de los bordes:
Calcula la magnitud de los bordes combinando las imágenes resultantes de los filtros Sobel mediante la fórmula de la magnitud Euclidiana.

Verificar si hay datos válidos en la matriz antes de normalizar:
Antes de normalizar la magnitud de los bordes, verifica si hay datos válidos en la matriz utilizando np.any.

Convertir a tipo de datos float32 antes de normalizar:
Convierte la matriz de magnitud de bordes a tipo de datos float32. Esto es necesario para evitar problemas de normalización con tipos de datos no compatibles.

Normalizar la imagen:
Utiliza el método de normalización para escalar los valores de la magnitud de los bordes al rango [0, 1]. Esto es importante para visualizar correctamente la imagen de bordes.

Mostrar la imagen con bordes:
Utiliza plt.imshow para mostrar la imagen resultante de la detección de bordes en escala de grises.
Muestra un título indicando que se ha aplicado el operador Sobel para la detección de bordes.

Manejar casos donde la matriz de magnitud de bordes está vacía:
Si la matriz de magnitud de bordes está vacía (todos los elementos son cero), imprime un mensaje indicando que la matriz está vacía o no contiene datos válidos.

En resumen, este programa carga una imagen, aplica el operador Sobel para detectar bordes y muestra la imagen resultante de la detección de bordes. Además, maneja casos donde la matriz de magnitud de bordes no contiene datos válidos.
Imágen de perfil

Programa para aplicación de filtros, en archivos de vídeo.


Python

estrellaestrellaestrellaestrellaestrella(4)
Actualizado el 20 de Noviembre del 2023 por Antonio (77 códigos) (Publicado el 24 de Mayo del 2021)
13.021 visualizaciones desde el 24 de Mayo del 2021
El presente programa se encarga de aplicar filtros sobre los fotogramas de un archivo de video empleando diferentes funciones. El programa realiza el filtrado frame a frame para a continuación generar un nuevo video con la secuencia de frames procesados (aplicando el frame rate del vídeo original). También usa el software "ffmpeg" para copiar el audio del vídeo original y añadirlo al vídeo resultante.

USO: Primeramente seleccionaremos el vídeo a filtrar mediante el botón "SEARCH". Una vez seleccionado iniciaremos el proceso con "START FILTERING" con el que empezaremos seleccionando la ubicación del nuevo vídeo, para a continuación iniciar el proceso (NOTA: La ruta del directorio de destino no deberá contener espacios en blanco). El proceso de filtrado podrá ser cancelado medinate el botón "CANCEL".
PARA CUALQUIER DUDA U OBSERVACIÓN USEN LA SECCIÓN DE COMENTARIOS.

vf
Imágen de perfil

Clasificación_Datos_por_Regresión Logística


Python

Publicado el 30 de Octubre del 2023 por Hilario (144 códigos)
629 visualizaciones desde el 30 de Octubre del 2023
Presentamos para nuestra aula, un sencillo ejercicio propuesto, para clasificar una serie de datos sintéticos, utilizando el sistema de regresión logística.
El ejercicio, es el siguiente:
Ejercicio_Clas_Regre_Log-Aula-28.py

La clasificación de datos por regresión logística es una técnica de aprendizaje automático que se utiliza para predecir la pertenencia de un conjunto de datos a una o más clases. Aunque el nombre "regresión" logística incluye la palabra "regresión", este enfoque se utiliza para problemas de clasificación en lugar de regresión.

La regresión logística se emplea cuando se desea predecir la probabilidad de que una observación pertenezca a una categoría o clase específica, generalmente dentro de un conjunto discreto de clases. Por lo tanto, es una técnica de clasificación que se utiliza en problemas de clasificación binaria (dos clases) y clasificación multiclase (más de dos clases). Por ejemplo, se puede usar para predecir si un correo electrónico es spam (clase positiva) o no spam (clase negativa) o para clasificar imágenes en categorías como gatos, perros o pájaros.

La regresión logística utiliza una función logística (también conocida como sigmoide) para modelar la probabilidad de pertenecer a una clase particular en función de variables de entrada (características). La función sigmoide tiene la propiedad de que produce valores entre 0 y 1, lo que es adecuado para representar probabilidades. El modelo de regresión logística utiliza coeficientes (pesos) para ponderar las características y calcular la probabilidad de pertenencia a una clase.

Durante el entrenamiento, el modelo busca ajustar los coeficientes de manera que las probabilidades predichas se ajusten lo más cerca posible a las etiquetas reales de los datos de entrenamiento. Una vez que se ha entrenado el modelo, se puede utilizar para predecir la probabilidad de pertenencia a una clase para nuevos datos y tomar decisiones basadas en esas probabilidades, como establecer un umbral para la clasificación en una clase específica.
*************************************************************************************************************
Los pasos que realizamos en el ejercicio, son los siguientes:

1-Generamos datos sintéticos donde la clase se determina por la suma de las dos características.
2-Implementamos la regresión logística desde cero sin el uso de scikit-learn, incluyendo el cálculo de 3-gradientes y la actualización de pesos.
4-Dibujamos los datos de entrada en un gráfico, junto con la línea de decisión que separa las clases.


En resumen, la regresión logística es una técnica de clasificación que modela las probabilidades de pertenencia a clases utilizando la función sigmoide y es ampliamente utilizada en una variedad de aplicaciones de aprendizaje automático.
Imágen de perfil

Ejercicio_Aula_23_Momentum


Python

Publicado el 26 de Octubre del 2023 por Hilario (144 códigos)
427 visualizaciones desde el 26 de Octubre del 2023
python3 Ejercicio_Aula_23_Momentum.py

Sencillo ejercicio sobre un descenso de gradiente con momento, (Gradient Descent with Momentum en inglés).
Se trata de aplicar este algoritmo a una funcion parabolica del tipo: f(x) = x^2 / 6.
Cuya derivada es:x**2 / 6.
El descenso de gradiente con momento es una variante del algoritmo de descenso de gradiente utilizado en la optimización y entrenamiento de modelos de aprendizaje automático, particularmente en el contexto de redes neuronales y problemas de optimización no convexos. Su objetivo es acelerar la convergencia del descenso de gradiente y ayudar a evitar quedarse atrapado en óptimos locales.

La principal diferencia entre el descenso de gradiente con momento y el descenso de gradiente estándar es la adición de un término de "momentum" o impulso. En el descenso de gradiente estándar, en cada iteración, el gradiente actual se utiliza directamente para actualizar los parámetros del modelo. En cambio, en el descenso de gradiente con momento, se mantiene un promedio ponderado exponencial de los gradientes anteriores y se utiliza ese promedio para actualizar los parámetros.

El objetivo del término de momento es suavizar las actualizaciones de los parámetros y reducir las oscilaciones que pueden ocurrir cuando el gradiente varía significativamente en diferentes direcciones. Esto puede ayudar a acelerar la convergencia y a sortear barreras o mínimos locales en la función de costo

En este sencillo ejercicio que propongo, en vez de utilizar datos sintéticos de caráctear aleatorio de entrada, lo vamos a aplicar a una función parabólica.


descarga
descarga-1
Imágen de perfil

Descenso de gradiente tipo Adam.


Python

Publicado el 19 de Octubre del 2023 por Hilario (144 códigos)
755 visualizaciones desde el 19 de Octubre del 2023
El descenso de gradiente tipo Adam, o simplemente Adam (por Adaptive Moment Estimation), es un algoritmo de optimización utilizado en el campo del aprendizaje automático y la inteligencia artificial para ajustar los parámetros de un modelo de manera que se minimice una función de pérdida. Adam es una variante del descenso de gradiente estocástico (SGD) que combina técnicas de otros algoritmos de optimización para mejorar la convergencia y la eficiencia en la búsqueda de los mejores parámetros del modelo.

Aquí hay una explicación simplificada de cómo funciona el algoritmo Adam:

Inicialización de parámetros: Se inician los parámetros del algoritmo, como la tasa de aprendizaje (learning rate), los momentos de primer y segundo orden, y se establece un contador de iteraciones.

Cálculo del gradiente: En cada iteración, se calcula el gradiente de la función de pérdida con respecto a los parámetros del modelo. Esto indica en qué dirección deben ajustarse los parámetros para reducir la pérdida.

Cálculo de momentos de primer y segundo orden: Adam mantiene dos momentos acumulativos, uno de primer orden (media móvil de los gradientes) y otro de segundo orden (media móvil de los gradientes al cuadrado).

Actualización de parámetros: Se utilizan los momentos calculados en el paso anterior para ajustar los parámetros del modelo. Esto incluye un término de corrección de sesgo para tener en cuenta el hecho de que los momentos se inicializan en cero. La tasa de aprendizaje también se aplica en esta etapa.

Iteración y repetición: Los pasos 2-4 se repiten durante un número especificado de iteraciones o hasta que se cumpla un criterio de parada, como la convergencia.

Adam se considera una elección popular para la optimización de modelos de aprendizaje profundo debido a su capacidad para adaptar la tasa de aprendizaje a medida que se entrena el modelo, lo que lo hace efectivo en una variedad de aplicaciones y evita problemas como la convergencia lenta o la divergencia en el entrenamiento de redes neuronales. Sin embargo, es importante ajustar adecuadamente los hiperparámetros de Adam, como la tasa de aprendizaje y los momentos, para obtener un rendimiento óptimo en un problema específico.
Imágen de perfil

Descenso Gradiente tipo Nesterov


Python

Publicado el 18 de Octubre del 2023 por Hilario (144 códigos)
384 visualizaciones desde el 18 de Octubre del 2023
Sencillo ejemplo de un descenso de gradiente del tipo Nesterov.

Descen_Grad_Nesterov_Aula_B_28_18_OCT_github.py
----------------------------------------------------------------------------------------------------

El descenso de gradiente tipo Nesterov, también conocido como el "descenso de gradiente acelerado de Nesterov" o "NAG" por sus siglas en inglés (Nesterov Accelerated Gradient Descent), es una variante del algoritmo de optimización de descenso de gradiente utilizado en el entrenamiento de redes neuronales y en la optimización de funciones en el aprendizaje automático.

Fue propuesto por Yurii Nesterov en 1983 y es una mejora con respecto al descenso de gradiente estándar, especialmente en términos de velocidad de convergencia. El descenso de gradiente Nesterov se diferencia del descenso de gradiente tradicional en cómo se actualizan los parámetros del modelo.

En el descenso de gradiente Nesterov, en lugar de calcular el gradiente de la función de costo en la posición actual de los parámetros, se calcula el gradiente en una posición ligeramente adelantada de los parámetros. Luego, se utiliza ese gradiente para realizar la actualización de los parámetros. Esto tiene el efecto de "mirar hacia adelante" antes de dar el paso de actualización, lo que puede ayudar a reducir la oscilación y mejorar la velocidad de convergencia.

La fórmula para la actualización de los parámetros en el descenso de gradiente tipo Nesterov es la siguiente:

v = γ * v - η * ∇J(θ - γ * v)
θ = θ + v

Donde:

θ son los parámetros del modelo.
∇J(θ - γ * v) es el gradiente de la función de costo evaluado en la posición adelantada de los parámetros.
v es una especie de "momentum" que acumula la velocidad de los pasos anteriores.
η es la tasa de aprendizaje.
γ es un hiperparámetro que controla la influencia del momentum en la actualización.
En resumen, el descenso de gradiente tipo Nesterov es una técnica de optimización que tiene la ventaja de converger más rápidamente que el descenso de gradiente estándar, lo que lo hace especialmente útil en el entrenamiento de redes neuronales profundas y otros problemas de optimización en el aprendizaje automático.



Imágen de perfil

Clasificacion de Datos Arboles de Decision


Python

Publicado el 17 de Octubre del 2023 por Hilario (144 códigos)
621 visualizaciones desde el 17 de Octubre del 2023
CuadernoAula-B-28-OCT-18.py
-----------------------------------------------------------------------------
La clasificación de datos mediante árboles de decisiones es un método de aprendizaje automático que se utiliza para categorizar o etiquetar datos en diferentes clases o categorías. Es una técnica de modelado predictivo que se basa en la creación de un "árbol" de decisiones, donde cada nodo interno del árbol representa una pregunta o una prueba sobre una característica específica de los datos, y las ramas que salen de ese nodo conducen a diferentes resultados o decisiones basadas en el valor de esa característica. Los nodos hoja del árbol representan las categorías o clases en las que se divide el conjunto de datos.

El proceso de clasificación a través de árboles de decisión implica:

Construcción del árbol: Se inicia con un nodo raíz que representa todo el conjunto de datos. Luego, se selecciona una característica y un umbral que se utilizará para dividir los datos en dos subconjuntos. Este proceso se repite recursivamente en cada subconjunto hasta que se alcanza un criterio de parada, como un tamaño máximo de profundidad del árbol, una cantidad mínima de muestras en los nodos hoja, o una impureza mínima.

Selección de características: En cada paso de división, se elige la característica que mejor separa los datos, lo que se logra al minimizar alguna métrica de impureza, como el índice de Gini o la entropía. La característica y el umbral que minimizan la impureza se utilizan para dividir los datos en dos ramas.

Predicción: Una vez construido el árbol, se utiliza para hacer predicciones sobre datos nuevos. Los datos nuevos se introducen en el árbol, siguiendo las ramas que corresponden a las características de esos datos, hasta llegar a un nodo hoja que representa la clase predicha.

Los árboles de decisión son atractivos porque son interpretables y fáciles de visualizar. Sin embargo, pueden ser propensos al sobreajuste (overfitting), especialmente si se construyen árboles muy profundos. Para abordar este problema, se pueden utilizar técnicas como la poda (pruning) o el uso de bosques aleatorios (random forests) que combinan múltiples árboles para mejorar la precisión y reducir el sobreajuste.

En resumen, la clasificación de datos mediante árboles de decisión es una técnica poderosa y ampliamente utilizada en aprendizaje automático para tareas de clasificación, donde el objetivo es predecir la categoría o clase a la que pertenecen los datos de entrada en función de sus características.
Imágen de perfil

Historial de Costos. Descenso estocástico


Python

Publicado el 17 de Septiembre del 2023 por Hilario (144 códigos)
453 visualizaciones desde el 17 de Septiembre del 2023
Ejercicio sencillo para aprendizaje de un descenso de gradiente tipo estocástico.
----------------------------------------------------------------------------------------------------------
Descenso de Gradiente Estocástico (Stochastic Gradient Descent, SGD):

El descenso de gradiente estocástico es un enfoque de optimización en el que se actualizan los parámetros del modelo utilizando un solo ejemplo de entrenamiento o un pequeño subconjunto de ejemplos (mini-batch) en cada iteración.

En cada iteración, se selecciona aleatoriamente un ejemplo o un mini-batch para calcular el gradiente y actualizar los parámetros.

SGD es mucho más eficiente computacionalmente que el muestreo histórico de costos y es especialmente útil cuando se tienen grandes conjuntos de datos, ya que permite un entrenamiento más rápido y escalable.

En resumen, el muestreo histórico de costos utiliza todo el conjunto de datos en cada iteración, mientras que el descenso de gradiente estocástico utiliza un subconjunto aleatorio de datos en cada iteración. SGD tiende a ser más ruidoso debido a su aleatoriedad, pero puede converger a una solución aceptable en menos iteraciones. Ambos enfoques tienen sus ventajas y desventajas, y la elección entre ellos depende de las características del problema y los recursos computacionales disponibles. También existen variantes intermedias, como el Mini-batch Gradient Descent, que utilizan un tamaño de mini-batch moderado para combinar eficiencia y estabilidad en el entrenamiento de modelos.
1...Anterior1234567891011Siguiente...74