Mostrar los tags: plot

Propongo el sencillo ejercicio en phyton : Aula_28_Ag.24_Espectro_Masas.py. Este ejercicio elabora una pequeña simulación planteando una espectrometría de una molécula de agua. Explicaremos, previamente un poco, en que consiste las espectrometría de masas.
-----------------------------------------------------------------------------------------------------------------------------------

La espectrometría de masas (MS, por sus siglas en inglés) es una técnica analítica utilizada para medir la relación masa/carga (m/z) de los iones presentes en una muestra. En el contexto de una molécula, como la del agua (H₂O), la espectrometría de masas permite identificar y cuantificar los fragmentos iónicos que resultan de la ionización de la molécula, lo que a su vez proporciona información sobre su estructura molecular y su composición.

Principios Básicos de la Espectrometría de Masas

Ionización:
-------------
La muestra, que puede ser un sólido, líquido o gas, se introduce en el espectrómetro de masas, donde se somete a un proceso de ionización. Este proceso convierte las moléculas en iones cargados (generalmente positivos) al agregar o quitar electrones.
Existen varios métodos de ionización, como la ionización por impacto electrónico (EI), electrospray (ESI), y ionización química (CI), entre otros.

Aceleración:
---------------
Los iones generados se aceleran mediante un campo eléctrico, de modo que todos los iones con la misma carga tengan la misma energía cinética.

Deflexión:
------------
Los iones acelerados pasan a través de un campo magnético o eléctrico que los desvía en función de su relación masa/carga (m/z). Los iones más ligeros y con una mayor carga se desvían más que los iones más pesados.

Detección:
-------------
Los iones desviados impactan en un detector que mide la intensidad de la señal, la cual está relacionada con la cantidad de iones presentes. La intensidad se registra para cada valor de m/z, generando así un espectro de masas.
Interpretación del Espectro de Masas

El resultado de la espectrometría de masas es un gráfico denominado espectro de masas, donde:

Eje X: Representa la relación masa/carga (m/z) de los iones.
Eje Y: Representa la intensidad o abundancia relativa de los iones detectados.
Cada pico en el espectro corresponde a un ion con una relación m/z específica. La altura del pico indica la cantidad relativa de ese ion en la muestra.

Aplicación a la Molécula de Agua (H₂O)
-----------------------------------------------------------
Para una molécula simple como el agua, la espectrometría de masas puede revelar varios iones, dependiendo del método de ionización:
----------------------------------------------------------------------------------------------------------------------------------
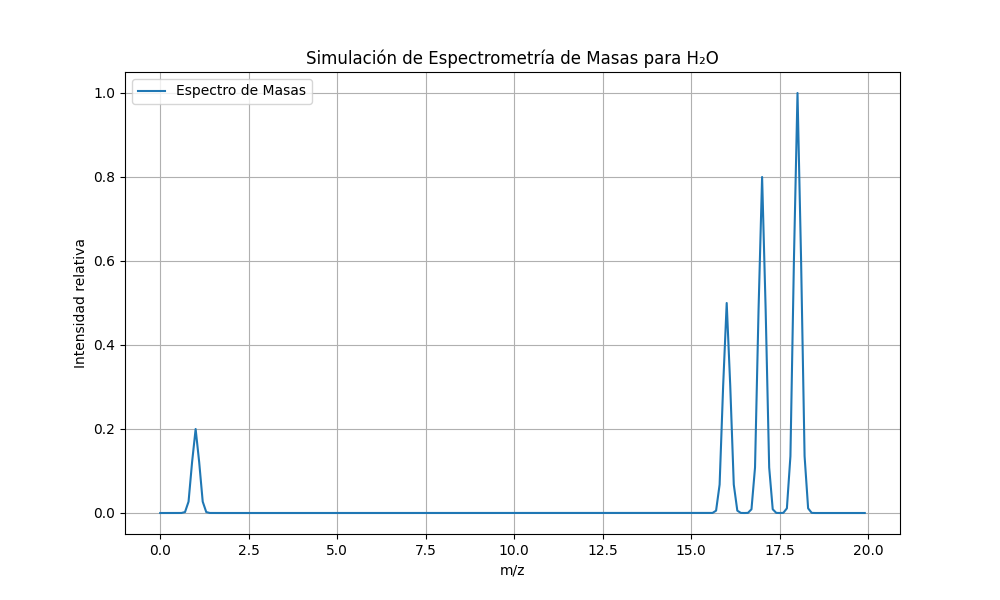
H₂O⁺ (m/z = 18): Ion molecular de agua sin fragmentar.
OH⁺ (m/z = 17): Fragmento ionizado que resulta de la pérdida de un átomo de hidrógeno.
O⁺ (m/z = 16): Ion de oxígeno, que podría resultar de la fragmentación de la molécula.
H⁺ (m/z = 1): Ion de hidrógeno.
En un espectro de masas de agua, podrías ver picos en estos valores de m/z, reflejando la presencia de estos fragmentos iónicos.

Ejemplo de Uso en Química y Biología.
---------------------------------------------------
Identificación de Compuestos: Al comparar el espectro de masas de una muestra con espectros de referencia, los químicos pueden identificar compuestos desconocidos.
Determinación de Estructuras Moleculares: La forma en que una molécula se fragmenta puede proporcionar pistas sobre su estructura química.
Cuantificación de Análisis: La espectrometría de masas también se usa para cuantificar la cantidad de un compuesto en una muestra, especialmente en el análisis de mezclas complejas.
Conclusión
La espectrometría de masas es una herramienta poderosa para estudiar las propiedades de las moléculas al identificar sus fragmentos iónicos y medir sus relaciones masa/carga. En la práctica, esta técnica tiene aplicaciones en química, biología, farmacología y muchas otras disciplinas científicas.

******************************************************************************************



Simulación del Espectro de Masas
--------------------------------------------------------
El espectro de masas para una molécula de agua podría incluir los siguientes iones:

H₂O → m/z = 18 (ion molecular)
OH → m/z = 17
O → m/z = 16
H → m/z = 1



Explicación del Código:
Fragmentos y sus m/z: Definimos las relaciones m/z para diferentes fragmentos posibles de la molécula de agua (H2O+, OH+, O+, H+).

Intensidades Relativas: Asignamos intensidades relativas a estos picos basadas en la probabilidad de fragmentación.

Espectro Simulado: Generamos un espectro de masas añadiendo picos gaussianos centrados en los valores de m/z definidos.

Visualización: El gráfico muestra la relación masa/carga (m/z) en las abscisas y la intensidad relativa en las ordenadas.

Resultado:
Al ejecutar este código, obtendrás un gráfico que simula un espectro de masas para una molécula de agua, donde se visualizan los diferentes iones generados por la fragmentación de la molécula. Este es un modelo simplificado, pero proporciona una base para entender cómo se podrían visualizar los datos obtenidos en un espectrómetro de masas.
-------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------
El ejercicio fue realizado en una plataforma linux. Concretamente en: Ubuntu 20.04.6 LTS.
Fue editado con Sublime text.
Ejecutado bajo consola Linux con el siguiente comando:
python3 Aula_28_Ag.24_Espectro_Masas.py

Se deberán tener cargados los siguientes módulos:
import numpy as np
import matplotlib.pyplot as plt

Ejecutado con python en versión:3
-------------------------------------------------------

****************************************************************************************
-----------------------------------------------------------------------------------------------------


Gráfica_integral_Aula_28.py
********************************
Por petición de varios alumnos del Aula 28. Proponemos hoy el siguiente ejercicio en python, donde explicamos el concepto de la integración, como contrario a la derivación, mostrando gráficamente los resultados. Con el mismo, pretendemos que los alumnos, repasen este concepto matématico, y al mismo tiempo, se familiaricen con los gráficos en el potente lenguaje python, de los mejores en este aspecto.

Básicamente dentro del cálculo matemático, podemos decir, de la forma más sencilla posible que:

La integración en matemáticas es una operación que permite calcular el área bajo una curva o función. En términos sencillos, imagina que tienes un gráfico y quieres saber el espacio que ocupa una parte de él, por ejemplo, el área entre la curva y el eje horizontal (el eje x). La integración te ayuda a encontrar ese área de forma precisa.

Por ejemplo, si tienes una función que describe la velocidad de un coche a lo largo del tiempo, la integración de esa función te dirá la distancia total que ha recorrido el coche en ese periodo de tiempo.

La integración es la inversa de la derivación. Mientras que la derivada de una función te da la pendiente o la tasa de cambio de esa función, la integral te da el acumulado de esa tasa de cambio.

La integración es un concepto fundamental del cálculo y del análisis matemático. Se puede pensar en ella como la operación inversa a la derivación.

Interpretaciones geométricas:
Área bajo la curva: La integral definida de una función f(x) entre a y b representa el área encerrada entre la gráfica de f(x), el eje x y las líneas verticales x = a y x = b.

Acumulación:
La integral definida de una función f(x) entre a y b puede interpretarse como la acumulación de la cantidad f(x) a lo largo del intervalo [a, b].

Definición formal:
Integral indefinida: La integral indefinida de una función f(x) se define como la función F(x) cuya derivada es f(x). Se escribe como ∫ f(x) dx.

Integral definida:
La integral definida de una función f(x) entre a y b se define como el límite de las sumas de Riemann cuando el número de subintervalos tiende a infinito. Se escribe como ∫_a^b f(x) dx.

Aplicaciones:
La integración tiene una gran variedad de aplicaciones en matemáticas, física, ingeniería y otras áreas. Entre ellas se encuentran:

*Cálculo de áreas, volúmenes y longitudes de curvas.
*Estudio del movimiento de objetos.
*Análisis de circuitos eléctricos.
*Probabilidad y estadística.
*etc

BREVE DESCRIPCIÓN DE LO QUE HACE EL EJERCICIO.
********************************************************************

Aunque el código va siendo explicado en cada paso del ejercicio.Para no redundar a continuación os pongo los pasos más importantes del código.

*Definimos una función que vamos a integrar.
*Calculamos el área bajo la curva de esa función entre dos puntos.
*Generamos puntos para dibujar la función.
*Dibujamos la función en una gráfica.
*Sombreamos el área bajo la curva para mostrar visualmente la integral.
*Añadimos una etiqueta que muestra el área total calculada.
*Dividimos el área en pequeños segmentos y calculamos el área de cada uno.
*Etiquetamos los segmentos en la gráfica para mostrar sus áreas individuales.
*El gráfico final muestra la función, el área total bajo la curva y las áreas de pequeños segmentos, ayudando a entender cómo se suma el área total.

**********************************************************************************************************************

Repaso-matplotlib-Aula-38-uranio-235.py
------------------------------------------------------
Con la idea de repasar la librería matplotlib, propongo este sencillo ejercicio de la representación aleatoria de un átomo de Uranio-235.
El ejercicio es de ejecución sencilla, y puede el alunno jugar con sus datos de entrada.
La librería matplotlib, es de uso habitual en todos los programas graficados, incluidos
los de inteligencia artificial.
----------------------------------------------------------------------------------------
Vamos a dar una pequeña descripción de Física cuántica, con el fin de entender este desarrollo.
********************************************************************************************
En la física cuántica, la idea de electrones orbitando alrededor del núcleo en trayectorias definidas, como planetas alrededor del sol, es incorrecta y ha sido reemplazada por un modelo más complejo y preciso.

En el modelo cuántico, los electrones no tienen órbitas definidas. En cambio, se describen mediante funciones de onda, que son soluciones a la ecuación de Schrödinger. Estas funciones de onda no nos dicen la trayectoria exacta de un electrón, sino la probabilidad de encontrar un electrón en una determinada región del espacio alrededor del núcleo. Esta región donde es más probable encontrar al electrón se llama "orbital".

Los orbitales tienen diferentes formas y tamaños, y cada uno corresponde a un nivel de energía específico. Los orbitales son esféricos, los p tienen forma de mancuerna, los d y f son más complejos. La densidad de probabilidad, que es la interpretación de la función de onda, nos da una "nube electrónica" donde la densidad de esta nube es mayor en las regiones donde es más probable encontrar al electrón.

En resumen:

Modelo Cuántico: En lugar de órbitas definidas, los electrones existen en "nubes de probabilidad" llamadas orbitales.
Funciones de Onda: Describen la probabilidad de encontrar un electrón en una determinada región del espacio.
Orbitales: Las diferentes formas (s, p, d, f) corresponden a diferentes distribuciones de probabilidad y niveles de energía.
Así que, efectivamente, los electrones están en un estado de movimiento continuo y no podemos determinar su posición exacta, sino solo la probabilidad de encontrarlo en un lugar determinado en un momento dado.


********************************************************************

Podemos crear una visualización simple utilizando la biblioteca matplotlib en Python para representar el núcleo atómico y una nube de electrones en movimiento aleatorio. A continuación, os presento el código Repaso-matplotlib-Aula-38-uranio-235.py
para crear esta simulación:

Este código hace lo siguiente:

Configuración inicial: Define el número de electrones y el límite del espacio donde se moverán.
Posiciones iniciales: Genera posiciones iniciales aleatorias para los electrones dentro de un cubo centrado en el núcleo.
Gráfico: Configura el gráfico 3D utilizando matplotlib.
Núcleo y electrones: Dibuja el núcleo en el centro y los electrones en sus posiciones iniciales.
Función de actualización: Mueve los electrones aleatoriamente en cada fotograma, asegurándose de que permanezcan dentro de los límites definidos.
Animación: Utiliza FuncAnimation de matplotlib para animar el movimiento de los electrones.
Este es un modelo simplificado y no representa fielmente la mecánica cuántica, pero da una buena visualización de un núcleo y una nube de electrones moviéndose aleatoriamente alrededor
de él.

*****************************************************************************************

Umbral de órbita extrema: Se define una variable umbral_extremo que establece el límite a partir del cual consideramos que un electrón está en la órbita extrema.
Función de actualización:
Se calcula la distancia de cada electrón al núcleo usando np.linalg.norm.
Se separan los electrones en dos grupos: normales y extremos, según la distancia calculada.
Se limpian y vuelven a dibujar todos los elementos del gráfico en cada fotograma.
Se plotean los electrones normales en azul y los extremos en rosa.
Esto resaltará los electrones que están a punto de salirse de la órbita con un color rosa en la animación.

********************************************************************************************
Realizado en Linux, ubuntu.
Ejecución.
python3 Repaso-matplotlib-Aula-38-uranio-235.py

El presente programa muestra en una gráfica la evolución por días, del precio de un determinado valor, introducido por el usuario.
USO:
La información del valor se introducirá en el campo "Symbol:" (ejs: "GOOGL" para Google", "AAPL" para Apple, "TSLA" para Tesla...). Para un periodo en días que indicaremos en el campo "Time(days):" (predefinido para los últimos 90 días). Con los botones "High", "Low", "Open" y "Close", puede seleccionarse la información a mostrar (valor máximo, mínimo, de apertura y de cierre, estando el de cierre seleccionado por defecto). Con la opción "STYLE" puede cambiarse la apariencia de la gráfica. El botón "SHOW GRAPH" mostrará la gráfica en función de las entradas antes referidas. El botón "SHOW TABLE" mostrará la información en una tabla de valores (dicha tabla podrá guardarse en un documento de texto con el botón "SAVE TABLE"). Finalmente la información "BBbands" solo se muestra para determinados valores/Symbols.

Al iniciar el programa, se generará (si no está creado) un archivo, de nombre "symbols" en el que se irán almacenando las iniciales indicativas ("TSLA","^DJI","GOOGL","AAPL",NFLX","^IBEX"...) introducidas en consultas anteriores y que hayan generado algún resultado.

PARA CUALQUIER PROBLEMA, DUDA U OBSERVACIÓN, USEN LA SECCIÓN DE COMENTARIOS.

El siguiente script muestra el gráfico de velas, en el que se expresan los valores de cotización máximo, mínimo, de apertura y cierre, correspondientes a la la compañía "Apple" durante los últimos 90 días. Los datos se obtienen directamente de la página de "Yahoo finance".

Script para graficar funciones sencillas mediante la introducción del rango de X y la expresión a representar.

Código para solucionar interactivamente el cubo de rubik.


Permite especificar el numero de caras al ejecutarlo. Para crear un cubo de 5x5x5: