Mostrando del 1 al 10 de 14 coincidencias
Se ha buscado por el tag: artificial
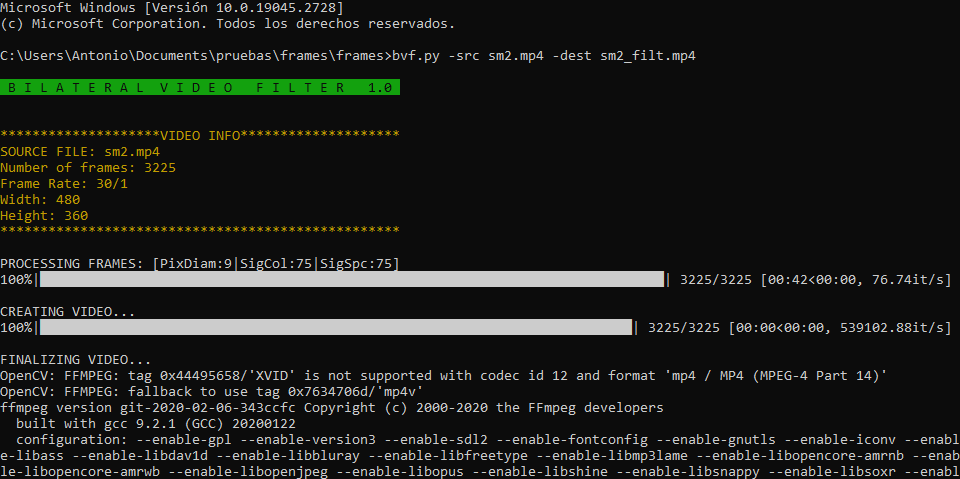
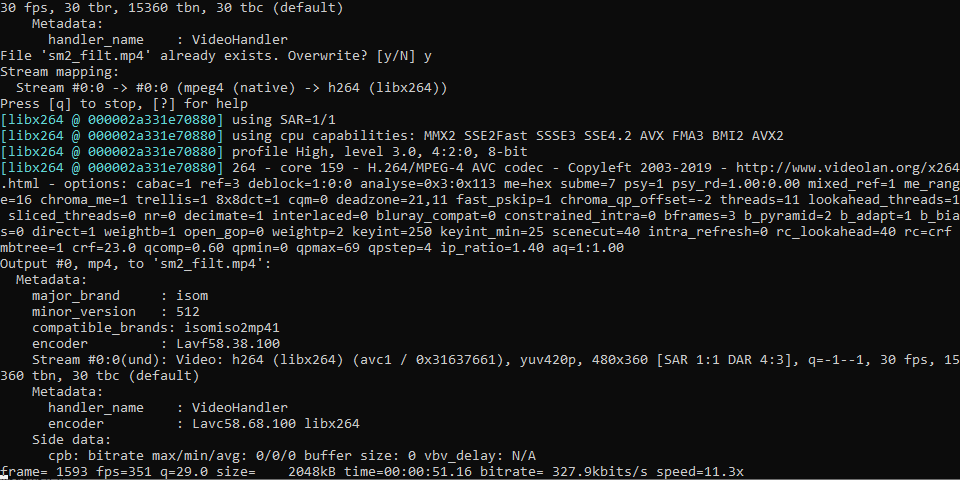
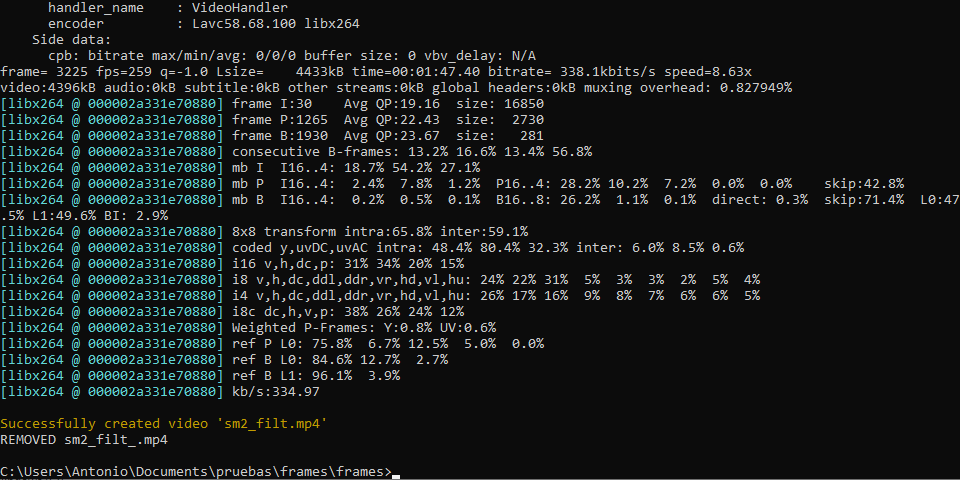
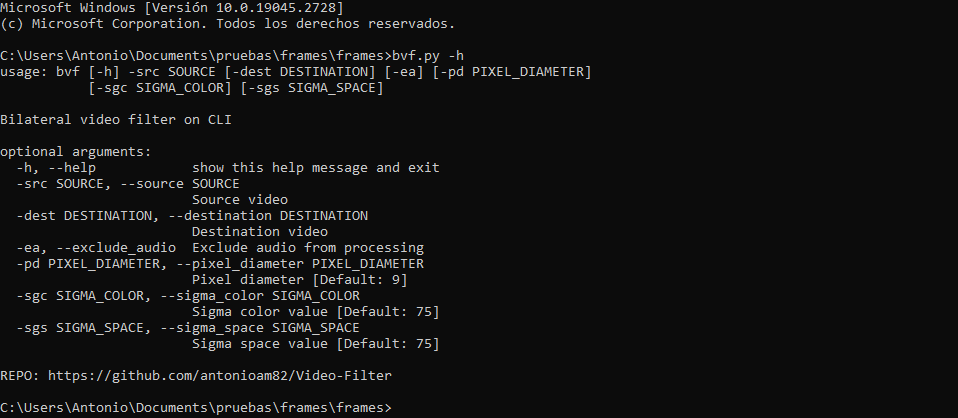
Programa para realizar filtrado de imagen en archivos de vídeo (preferiblemente de corta duración) utilizando el algoritmo de 'filtrado bilateral' pudiendo especificar los valores sigma de espacio y color y el diámetro del vecindario para cada pixel. Los vídeos filtrados se generan, por defecto, conservando su sonido, aunque se pueden generar sin este introduciendo el argumento '-ae'/'--exclude_audio'.
ARGUMENTOS:
-src/--source: Nombre del vídeo original (OBLIGATORIO)
-dest/--destination: Nombre del video a generar ('NewFilteredVid.mp4' por defecto)
-sgc/--sigma_color: Valor sigma para espacio de color (75 por defecto)
-sgs/--sigma_space: Valor sigma espacial (75 por defecto)
-pd/--pixel_diameter: Diámetro de la vecindad de píxeles (9 por defecto)
-ae/--exclude_audio: Excluir audio y generar video sin sonido (OPCIONAL)
PARA CUALQUIER DUDA U OBSERVACIÓN UTILIZEN LA SECCIÓN DE COMENTARIOS
Mi primer neur
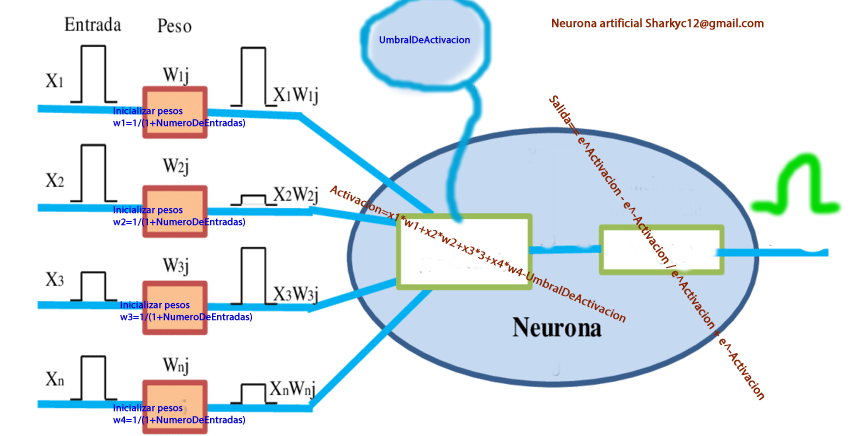
ona Perseptron, si bien desde el 2012 ya sabia hacer neuronas artificiales, yo estaba consciente que le faltaba algunas cosas.
No estaba 100% seguro de los conceptos.
En aquellos días era difícil ver tutoriales por video; hoy día es diferente, rápidamente se puede aprender viendo un video.
Nada como la comunicación verbal en combinación con el lenguaje corporal de un ser humano.
.
Dicha neurona es capaz de aprender, tiene todos los objetos que tiene una neurona, más un extra, la función de nacionalización de los pesos, con lo cual no es necesario usar un valor aleatorio.
MODELO DE PERCEPTRON SIMPLE
Los perceptrones son tipos de redes neuronales, las neuronal network más simples que existen. El modelo de perceptrón simple permite realizar una clasificación binaria de dos clases linealmente separables. Cada clase puede contener diferentes variables (X1 … Xn), cada una de estas variables supone una entrada a la red neuronal. Cada entrada se asocia a un determinado peso (W1 … Wn), el sumatorio del producto de cada entrada por su correspondiente peso nos da un valor, Z (z= Σ Xn*Wn ). Las diferentes entradas convergen en una misma neurona, esta representa la neurona de salida y tendrá un determinado umbral de activación, Y. Si el valor Z es mayor que el umbral de activación (Y) la neurona se activará y clasificará una clase como positiva, si por el contrario el valor Z no supera el umbral de activación Y, la neurona no se activará y clasificará la clase como negativa. El modelo de perceptrón simple requiere de un entrenamiento supervisado, es decir, para cada conjunto de valores le indicamos a que clase pertenecen dichos valores. De esta forma, cada vez que se equivoque al clasificar un conjunto de valores, se podrán ajustar los diferentes pesos W. A medida que esta red se va entrenando siempre convergerá en una solución, siempre y cuando, las dos clases sean LINEALMENTE SEPARABLES.
A continuación, vamos con un programa sumamente sencillo. En este programa, las dos clases contienen 4 variables las cuales, corresponden a números aleatorios en coma flotante comprendidos entre 0 y 1. Aparecen ajustados los intervalos (en la función al() ) para que ambas clases sean linealmente separables ya que si no, el programa nunca encontrará una solución. Los pesos del perceptrón han sido iniciados aleatoriamente en el intervalo de 0 a 0.5. Como mencioné anteriormente, se trata de un tipo de aprendizaje supervisado, por ello, para cada conjunto de datos se indica la clase a la que pertenece. Una vez que tenemos los datos a clasificar y los pesos del perceptrón inicializados aleatoriamente, el siguiente paso consiste en ajustan los pesos. Estos pesos se ajustarán solo cuando el clasificador falle siguiendo la función de entrenamiento (o algoritmo de aprendizaje) Wt+1 = Wt + (0 - Z)*Xn . Si el clasificador acierta la clase los pesos no se corrigen. Tras el entrenamiento el clasificador (en este caso en dos o tres ciclos) alcanza un rendimiento del 100%, de forma que todos los conjuntos de datos pertenecientes a la Clase 1 tienen un valor de Z > Y (superan el umbral de activación) y todos los datos pertenecientes a la Clase 2 tienen un valor de Z < Y (inferiores al umbral de activación).
Se trata de un algoritmo muy muy sencillo que representa el potencial de la Inteligencia Artificial en el análisis de datos. El umbral de activación o más formalmente la función de activación corresponde a la función más sencilla posible, la función escalón de McCulloch y Pitts. Estoy disponible para cualquier duda o sugerencia. Se que esto es un ejemplo sencillo, estaba practicando, diseñé e hice el programa en menos de una hora y decidí compartirlo por si a alguien le interesaba un poco el tema haciendo una mini-explicación.
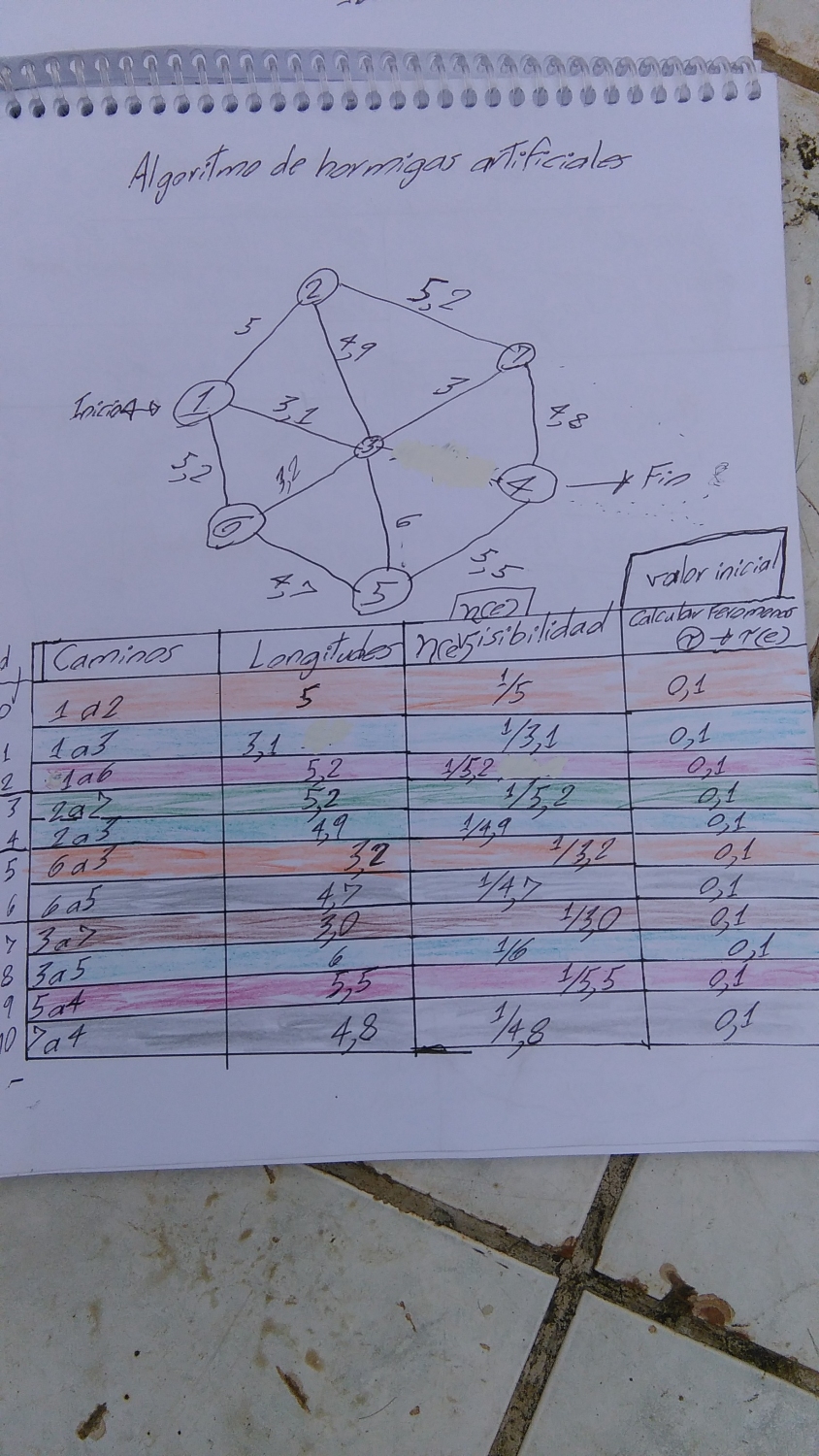
Son una serie de pruebas y practicas en MS Excel, de cuando estuve leyendo acerca de los algoritmos genéticos, de hormigas artificiales y gradiente descendente.
No es algo muy elegante, es más bien un borrador donde probaba los resultados antes de escribirlos en código de programación (En Java).
Pero esta lo suficientemente elaborado como para que se pueda implementar o usar como borrador para probarlo ya sea en el mismo Excel o en cualquier lenguaje de programación.
Finalmente, este archivo de MS Excel es una plantilla de MS Excel.
Neurona artificial con tres salidas diferentes.
Le he hecho una actualización a la neurona artificial normal; la actualización incluye la habilidad de ser trinaria y no binaria. O sea tiene el poder de lanzar: 1, 0, -1.
Ademas no pierde la habilidad de aprender.
Recuerden nosotros como humanos no somos binarios, somos trinarios o más todavía, nosotros usamos, si, no, talvez. Ya es hora que la computación tenga ese talvez, eso que nos hace humanos.
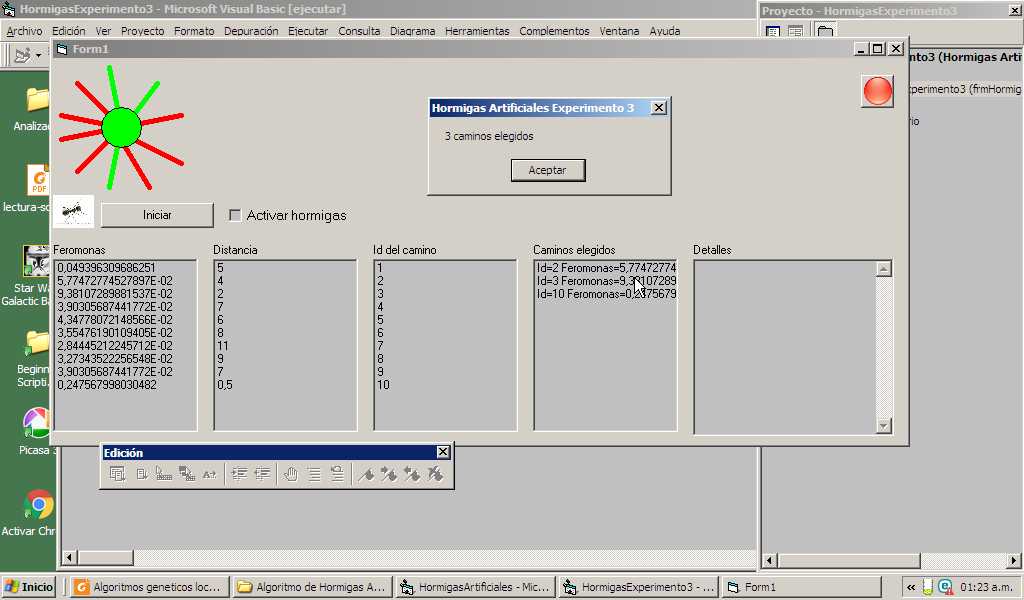
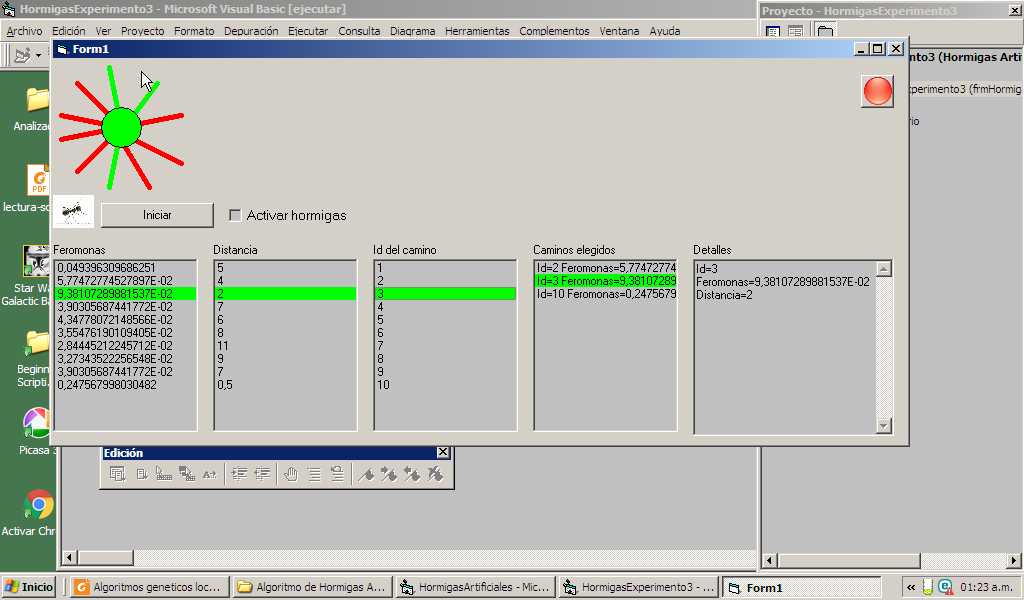
En este experimento numero 3 con el algoritmo de hormigas he obtenido un éxito rotundo.
Ya puedo usarlo para crear algún juego.
Solo espero tener el mismo éxito en redes neuronales y en algoritmos genéticos, campos en los que he tenido un éxito menor al 100%.
Pero con hormigas artificiales el éxito ha sido del 100%.
Esta vercion esta mejorada.
Es mucho más compacta.
