Código de Python - Orbitales

***********************************************************************************************************
-----------------------------------------------------------------------------------------------------------------------------
Proponemos este sencillo código: Aula_28_orbital.py . Con el fin de familiarizarmos con los entornos gráficos de Python.

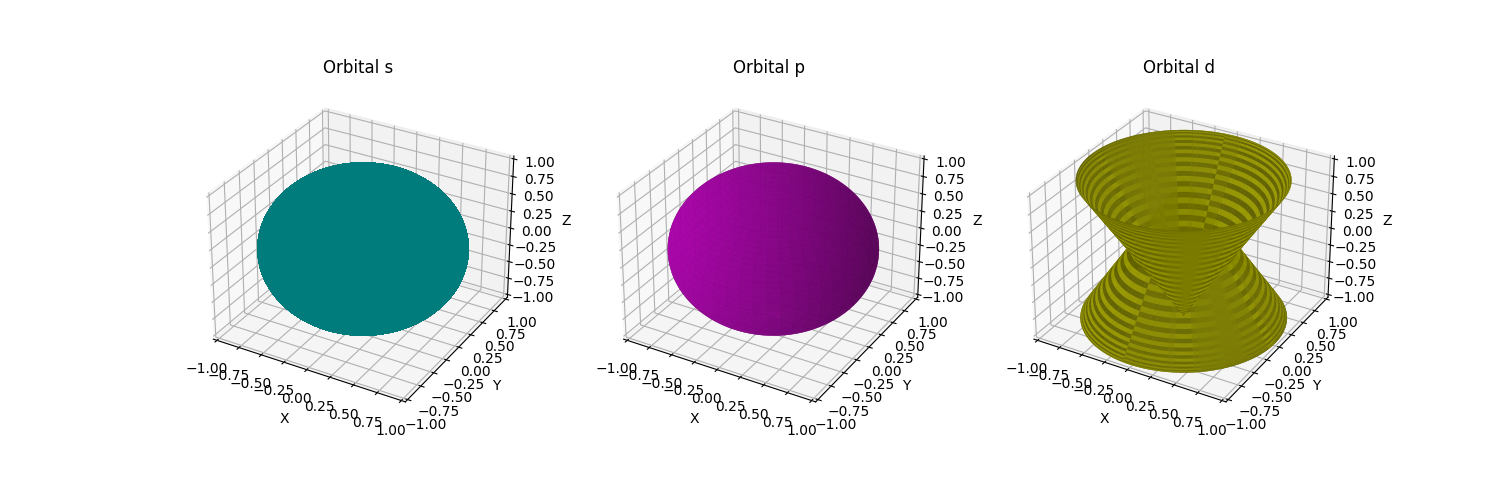
El código genera gráficos 3D de orbitales atómicos utilizando matplotlib y mpl_toolkits.mplot3d.
Este tipo de visualización es excelente para representar la forma de los orbitales s, p y d en tres dimensiones.

Aquí está el análisis del código y una revisión para asegurarnos de que funcione correctamente:

Importar módulos:

mpl_toolkits.mplot3d se importa para poder crear gráficos 3D.
matplotlib.pyplot se importa como plt para funciones de trazado.
numpy se importa como np para cálculos numéricos.

Crear la figura y los subgráficos:

Se crea una figura (fig) con tamaño de 15x5 pulgadas.
Se crean tres subgráficos (ax1, ax2, ax3) con proyección 3D.

Definir los datos de los orbitales:

Para el orbital s, se utilizan coordenadas esféricas.
Para el orbital p, se utilizan coordenadas que representan la forma lobular.
Para el orbital d, se utilizan coordenadas que representan una forma de doble lóbulo.

Trazar superficies:

Cada subgráfico (ax1, ax2, ax3) utiliza plot_surface para trazar la forma del orbital en el espacio 3D.
Se ajustan los límites de los ejes (set_xlim, set_ylim, set_zlim) para asegurar que todos los gráficos tengan la misma escala y sean comparables.

Configuración de etiquetas y títulos:

Se establecen etiquetas para los ejes (set_xlabel, set_ylabel, set_zlabel) y títulos (set_title) para cada subgráfico.

Mostrar el gráfico:

plt.show() se utiliza al final para mostrar la figura completa con los tres subgráficos.
El código parece estar bien estructurado para visualizar los orbitales s, p y d en 3D.
-----------------------------------------------------------------------------------------------------------------------
Asegúrate de tener matplotlib y numpy instalados en tu entorno de Python para que funcione correctamente.

-------------------------------------------------------------------------------------------------------
El ejercicio fue realizado en un entorno Linux.
Plataforma Ubuntu 20.04.6 LTS.
Editado con Sublime txt.